Binary Numbers#

Here is a visualization to help introduce the concept of binary numbers, and how any integer can be represented with just two states. Imagine you have four cards as pictured below. Each card has a number of dots on it. The right-most card has one dot, the next two dots, and so on so that each card has double the number of dots of the card on the right.

You can leave the cards with the dots chowing, or you can cover them up so there are no dots. Which cards would have to be covered to have the total number of dots showing be 7? 12?

Each card has two states. We represent “dots showing” with a 1, and “no dots” with a 0. With this system, 7 is 0111, and 12 is 1100.

Concept Check:

  1. With the cards above, what is the largest number of dots possible?

  2. What is the smallest?

  3. Are there any numbers in between that are not possible?

  4. If we had \(N\) cards, what would the range of possible values be?

Solution

  1. 15

  2. 0

  3. All numbers between 0 and 15 are possible. You can show this pretty easily with a proof by induction.

  4. 0 to \(2^N - 1\)

Binary is a base-2 numbering system, similar to the familiar base-10 (decimal) system. Just as a number written in the decimal system can be broken up into the “ones” (\(10^0\)), “tens” (\(10^1\)), and “hundreds” (\(10^2\)) etc. columns, binary numbers are broken up into the ones (\(2^0\)), twos (\(2^1\)), fours (\(2^2\)), etc. columns. In places where it may be confusing, I will use the subscript \(_{10}\) to denote a decimal number, and \(_2\) for a binary number.

When we write \(27_{10}\), this really means \(2 \times 10^1 + 7 \times 10^0\). We can convert binary to decimal in a similar way:

\[ 1011_2 = 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 0 + 2 +1 =11_{10} \]

Another approach is to use the “Double Dabble Method”, shown below again converting \(1011_2\). With this method, you successively double each binary digit starting from the left, and then add the next digit.

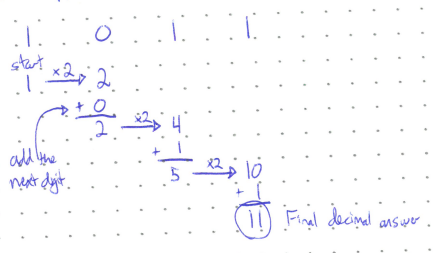
DoubleDabble

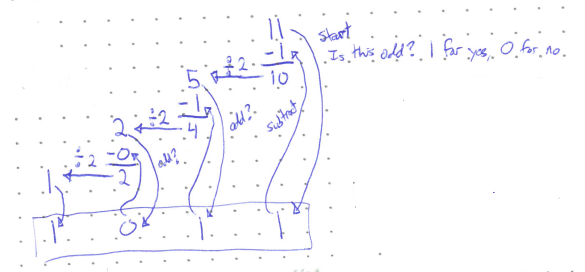
To convert from decimal to binary, you can essentially do the above backwards. Starting from the right this time, you ask if the number is odd, and if it is you put a 1 in the current column of the binary number and then subtract it from the decimal number. If not, put a 0 in the binary column. Next divide the decimal number by 2 and repeat for the next column.

decimalToBinary

Finally, there is some common terminology you need to be aware of when dicussing binary numbers.

Bit

Binary digit

Byte

8 bits

Most Significant Bit (MSB)

The left-most bit

Least Significant Bit (LSB)

The right-most bit (usually the “ones” column)